Catatan Via: Baris dan Deret Geometri

Geometri

Barisan Geometri mempunyai ciri-ciri memiliki perbandingan/rasio antara dua suku yang berurutan selalu sama atau tetap. Perhatikan dua contoh barisan Geometri di bawah yang meliputi barisan geometri naik dan barisan geometri turun.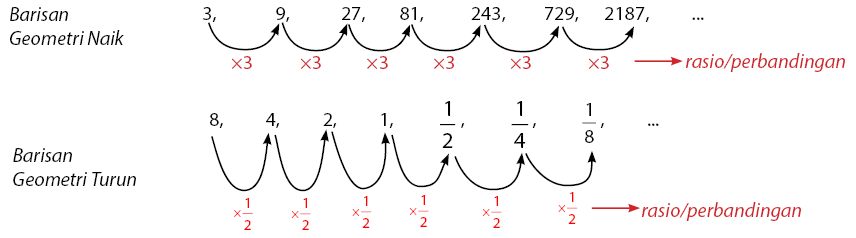

BarisanGeometri

Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.

Berdasarkan pola barisan aritmetika, terdapat rumus yang dapat digunakan untuk mempermudah mencari suku-n.

Rumus suku ke-n pada Barisan Geometri

$U_{n} = ar^{(n-1)}$

Keterangan:
$U_{n}$ = suku ke-n
a = suku pertama
r = rasio $= \frac{U_{n}}{U_{n-1}}$

Penjumlahan suku-suku pada barisan geometri membentuk sebuah deret yang disebut dengan deret geometri.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.

Jumlah n suku pertama pada Barisan Geometri
untuk r > 1

$S_{n} = \frac{a \left( r^{n} - 1 \right)}{r - 1}$

untuk r < 1

$S_{n} = \frac{a \left( 1 - r^{n} \right)}{1 - r}$

Keterangan:
$S_{n}$ = jumlah n suku pertama
$U_{n}$ = suku ke-n
a = suku pertama
r = rasio = $= \frac{U_{n}}{U_{n-1}}$

Contoh Soal dan Pembahasan
Seutas tali dipotong menjadi 5 bagian yang ukurannya membentuk deret geometri. Jika panjang potongan tali terpendek 4 cm dan panjang potongan tali terpanjang 324 cm, maka panjang tali semula adalah …. (SOAL UN MATEMATIKA SMP 2016)
A. 328 cm
B. 484 cm
C. 648 cm
D. 820 cm

Pembahasan:
Tali membuat Barisan geometri seperti terlihat pada gambar di bawah.