Catatan Via: Januari 2019

Kamis, 31 Januari 2019

¼ ABAD

Assalamu'alaikum wr wb...
Haiii selamat bertemu lagi 😊✌️

Ga kerasa ya kita ga pernah tulis menulis di blog ini lagi. Sekarang aku sudah menikah & alhamdulillah juga sudah punya anak laki2 yang InsyaaAllah sholeh 😇

Waktu berjalan begitu cepat, usiaku sekarang hampir ¼ abad. 12 Februari nanti, jika Allah masih memberiku umur panjang, umurku genap 25 tahun. Ah, aku benar2 malu.
Banyak hal yang masih harus aku perbaiki, terutama hal ke-imanan & ke-islamanku. Sebagai seorang istri juga sekaligus seorang ibu, aku masih belum bisa memberikan pelayanan yang baik yang sesuai dengan syariat islam. Mulai hari ini, bersamaan dengan kembalinya aku menulis lagi di blog ini, InsyaaAllah aku akan meng-upgrad segala hal yang kurang baik yang terlanjur menempel di jiwa ini. Mulai dari puasa Senin-Kamis. Kemudian dilanjut dengan solat sunah2 lainnya, terutaman kewajiban ku kepasa Allah SWT & keluarga. Semoga niat kembali berhijrah ini Allah mudahkan, agar ketika jiwa sudah tak lagi di badan, aku siap pergi dengan tenang. Bismillahirrahmanirrahim...

Selasa, 29 Januari 2019

Baris dan Deret Geometri

Geometri

Barisan Geometri mempunyai ciri-ciri memiliki perbandingan/rasio antara dua suku yang berurutan selalu sama atau tetap. Perhatikan dua contoh barisan Geometri di bawah yang meliputi barisan geometri naik dan barisan geometri turun.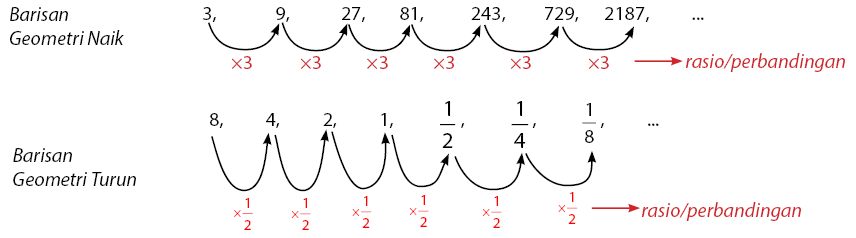

BarisanGeometri

Suku ke-n menunjuk pada suku pada urutan ke-n, lebih jelasnya dapat dilihat pada gambar berikut.

Berdasarkan pola barisan aritmetika, terdapat rumus yang dapat digunakan untuk mempermudah mencari suku-n.

Rumus suku ke-n pada Barisan Geometri

$U_{n} = ar^{(n-1)}$

Keterangan:
$U_{n}$ = suku ke-n
a = suku pertama
r = rasio $= \frac{U_{n}}{U_{n-1}}$

Penjumlahan suku-suku pada barisan geometri membentuk sebuah deret yang disebut dengan deret geometri.

Rumus di bawah dapat digunakan untuk mencari jumlah n suku pertama.

Jumlah n suku pertama pada Barisan Geometri
untuk r > 1

$S_{n} = \frac{a \left( r^{n} - 1 \right)}{r - 1}$

untuk r < 1

$S_{n} = \frac{a \left( 1 - r^{n} \right)}{1 - r}$

Keterangan:
$S_{n}$ = jumlah n suku pertama
$U_{n}$ = suku ke-n
a = suku pertama
r = rasio = $= \frac{U_{n}}{U_{n-1}}$

Contoh Soal dan Pembahasan
Seutas tali dipotong menjadi 5 bagian yang ukurannya membentuk deret geometri. Jika panjang potongan tali terpendek 4 cm dan panjang potongan tali terpanjang 324 cm, maka panjang tali semula adalah …. (SOAL UN MATEMATIKA SMP 2016)
A. 328 cm
B. 484 cm
C. 648 cm
D. 820 cm

Pembahasan:
Tali membuat Barisan geometri seperti terlihat pada gambar di bawah.

dengan
$U_{1}$ adalah tali terpendek = 4 cm
$U_{5}$ adalah sampai terpanjang = 324 cm
Sehingga,

$U_{5} = 324$

$ar^{4} = 324$

$4 \times r^{4} = 324$

$r^{4} = \frac{324}{4}$

$r^{4} = 81$

$r = 3$

Sehingga barisan geometrinya menjadi 4, 12, 36, 108, dan 324.
Panjang tali semula adalah 4 + 12 + 36 + 108 + 324 = 484 cm.

Senin, 28 Januari 2019

Fungsi Komposisi

Kamu pasti sudah tidak asing dengan istilah fungsi bukan? Fungsi adalah relasi himpunan A ke himpunan B, dengan setiap anggota A dipasangkan ke satu anggota B. Ketika ada dua fungsi yang digabungkan secara berurutan maka akan membentuk sebuah fungsi baru, inilah yang biasa disebut fungsi komposisi. Bagaimana ya penggabungan dua fungsi menggunakan fungsi komposisi? Simak penjelasan berikut ini ya.

Fungsi komposisi merupakan penggabungan operasi dua jenis fungsi f(x) dan g(x) sehingga menghasilkan sebuah fungsi baru. Operasi fungsi komposisi biasa dilambangkan dengan "o" dan dibaca komposisi atau bundaran. Fungsi baru yang dapat terbentuk dari f(x) dan g(x) adalah:

1. (f o g)(x) artinya g dimasukkan ke f

2. (g o f)(x) artinya f dimasukkan ke g

Fungsi tunggal tersebut merupakan fungsi yang dapat dilambangkan dengan huruf “f o g” atau juga dapat dibaca “fungsi f bundaran g”. Fungsi “f o g” adalah fungsi g yang dikerjakan terlebih dahulu kemudian dilanjutkan dengan f. Sedangkan, untuk fungsi “g o f” dibaca fungsi g bundaran f. Jadi, “g o f” adalah fungsi dengan f dikerjakan terlebih dahulu daripada g.

Untuk memahami fungsi ini, perhatikan gambar berikut:

Dari rumus di atas, definisi yang kita dapatkan adalah :

Jika f : A → B ditentukan dengan rumus y = f(x)

Jika g : B → C ditentukan dengan rumus y = g(x)

Maka, didapatkan hasil fungsi g dan f:

h(x) = (gof)(x) = g( f(x))

Dari penjelasan di atas dapat disimpulkan bahwa fungsi yang melibatkan fungsi f dan g dapat ditulis :

(g o f)(x) = g(f(x))
(f o g)(x) = f(g(x))

Terdapat sifat-sifat pada fungsi komposisi yang dijelaskan pada gambar di bawah ini.

Jika f : A → B , g : B → C , h : C → D, maka berlaku :

kerjakan contoh soal di bawah ini supaya kamu semakin mengerti dengan fungsi komposisi.

1. Jika f(x) = 2x + 3 dan (f o g) = 2x² + 6x – 7, maka berapakah hasil dari g(x) ?