Materi Pengantar Dimensi Tiga

Definisi

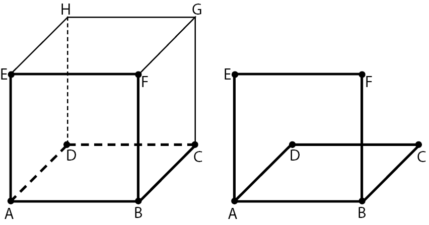
Dimenasi tiga merupakan bangun dengan ukuran yang terdiri atas panjang, lebar, dan tinggi. Dimensi tiga juga sering disebut juga dengan bangun ruang. Materi dimensi tiga yang akan dibahas pada halaman ini meliputi unsur dimensi tiga yang akan sering disebut ketika membahas materi dimensi tiga nantinya. Unsur tersebut adalah diagonal sisi, diagonal ruang, bidang frontal, dan bidang diagonal. Unsur tersbut dapat dilihat pada gambar di bawah.

Selain itu, juga akan diulas materi tentang kedudukan antar titik, garis, dan bidang. Hubungan kedudukan pada materi dimensi tiga meliputi kedudukan antar titik, garis, dan bidang. Kedudukan titik yang akan dibahas pada materi dimensi tiga adalah kedudukan titik pada garis, kedudukan titik di luar garis, kedudukan titik pada bidang, dan kedudukan titik di luar bidang.

Perhatikan gambar kubus di bawah!

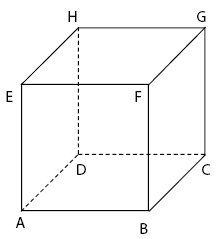
Kubus disusun atas 8 titik sudut, 12 rusuk sebagai garis, dan 6 persegi sebagai bidang. Cakupan materi dimensi tiga yang akan diulas meliputi pengertian kedudukan antar kompenen penyusun kubus tersebut.

Kedudukan Titik

1. Titik Terletak pada Garis
   Contoh: Titik A dan Garis AB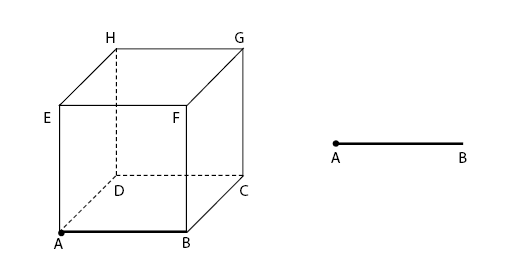
   
2. Titik Terletak di Luar Garis
   Contoh: Titik C dan garis AB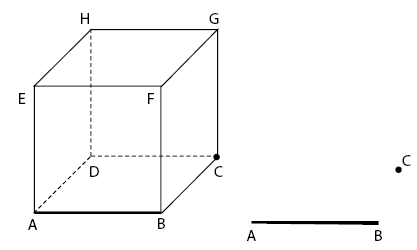
   


3. Titik Terletak pada Bidang
   Contoh: Titik A dan bidang ABCD
   
4. Titik Terletak di luar Bidang
   Titik E dan bidang ABCD
   

Kedudukan Dua Garis

Sebelum masuk pada pembahasan kedudukan garis pada bidang, mari mengulang materi kedudukan dua garis terlbih dahulu. Kedudukan dua garis terdiri atas berimpit, berpotongan, sejajar, dan bersilangan. Simak uraian masing-masing pada pembahasan di bawah.

1. Berimpit
   Sebuah garis dikatakan berimpit jika kedua garis saling bersekutu.
   Contoh: garis AB dan garis AB
   


2. Berpotongan
   Kedua garis dikatakan berpotongan jika mempunyai satu titik persekutuan yang disebut dengan titik potong.
   Contoh: Garis AB dan AD
   


3. Sejajar
   Kedua garis dikatakan sejajar jika dua garis itu terletak pada satu bidang dan tidak mempunyai titik persekutuan.
   Contoh garis AB dan EF
   


4. Bersilangan
   
   Kedua garis dikatakan bersilangan jika dua garis itu tidak sejajar sekaligus tidak berpotongan.
   Contoh: Garis EH dan AB
   

Kedudukan Antara Garis pada Bidang

Kedudukan antara garis pada bidang meliputi kedudukan garis terletak pada bidang, kedudukan garis memotong bidang, dan kedudukan garis sejajar bidang. Langsung simak uraian masing-masing pada pembahasan di bawah.

1. Garis Terletak pada Bidang
   Sebuah garis dikatakan terletak pada bidang jika setiap titik pada garis tersebut terletak juga pada bidang.
   Contoh: garis CD dan bidang ABCD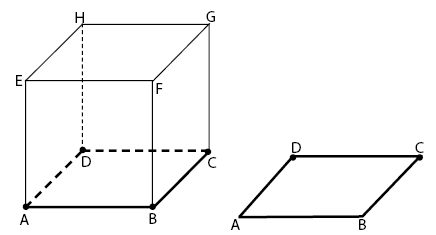
   
2. Garis Memotong Bidang
   Sebuah garis dikatakan memotong bidang jika garis dan bidang tersebut mempunyai satu titik persekutuan yang disebut titik potong/titik tembus.
   Contoh: garis BC menembus bidang ABFE di titik B.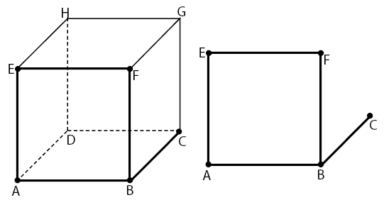
   


3. Garis Sejajar dengan Bidang
   Garis dikatakan sejajar dengan bidang jika garis dan bidang tersebut tidak mempunyai titik persekutuan atau titik potong.
   Contoh: garis GH dan bidang ABFE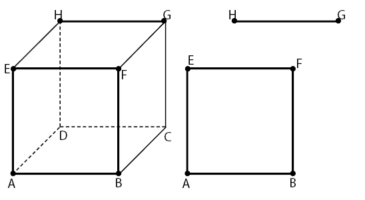
   



Kedudukan Antara Bidang dan Bidang

Pembahasan materi dimensi tiga selanjutnya adalah kedudukan antara bidang dan bidang. Keudukan antara dua bidang meliputi berimpit, sejajar, dan berpotongan. Untuk lebih jelasnya, simak uraian masing-masing pada pembahasan di bawah.

1. Berimpit
   Dua bidang dikatakan berimpit jika kedua bidang tersebut saling bersekutu.
   Contoh: bidang ABFE dan bidang ABFE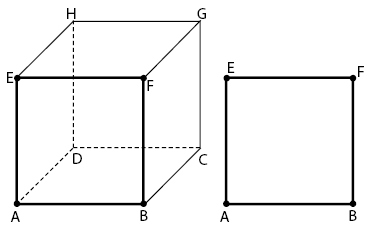
   


2. Sejajar
   Dua bidang dikatakan sejajar jika kedua bidang tersebut tidak bersekutu pada satu titik manapun.
   Contoh: bidang ABFE dan bidang DCGH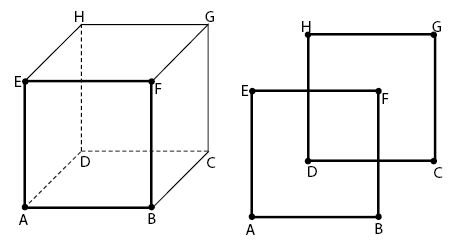
   


3. Berpotongan
   Dua bidang dikatakan berpotongan jika kedua bidang itu mempunyai sebuah garis persekutuan atau garis perpotongan.
   Contoh: bidang ABCD dan bidang ABFE