Jarak Titik ke Titik (Jarak Dua Titik)
Jarak dua titik dinyatakan sebagai panjang garis yang menghubungkan kedua titik tersebut. Untuk mencari jarak antara dua titik yang diketahui keterangan panjang, cara yang umum digunakan dapat menggunakan rumus pythagoras.
Terkadang, ada bentuk soal yang menanyakan jarak dua titik hanya diketahui koordinatnya. Jika kedua letak koordinatnya dinyatakan sebagai (x, y, z) maka dapat dicari menggunakan cara dan rumus mencari pada dimensi tiga, seperti kasus berikut.
Diketahui dua titik A dan B dengan koordinat berturut-turut adalah  dan
dan  . Jarak titik A dan B dapat dicari menggunakan rumus berikut.
. Jarak titik A dan B dapat dicari menggunakan rumus berikut.
Berikut ini akan diberikan contoh soal mencari jarak titik ke titik yang terletak pada bangun ruang untuk menambah pemahaman sobat idschool.
Contoh Soal dan Pembahasan Jarak Titik ke Titik
Contoh 1: Tentukan jarak antara dua titik yang memiliki koordinat P(0, 7, 6) dan Q(5, 2, 1)!
Contoh 1: Tentukan jarak antara dua titik yang memiliki koordinat P(0, 7, 6) dan Q(5, 2, 1)!
Pembahasan:
Contoh 2:
Perhatikan gambar berikut!
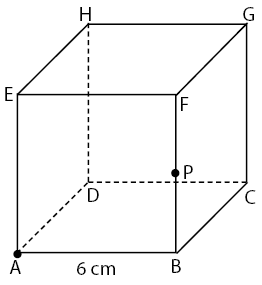
Jika titik P berada pada tengah-tengah garis BF maka jarak antara titik A dan P adalah ….
A.
B.
C.
D.
E.

Jika titik P berada pada tengah-tengah garis BF maka jarak antara titik A dan P adalah ….
A.
B.
C.
D.
E.
Pembahasan:
Perhatikan gambar di bawah!

Panjang  dengan menggunakan rumus phytagoras, kita akan peroleh nilai AP seperti terlihat pada cara berikut.
dengan menggunakan rumus phytagoras, kita akan peroleh nilai AP seperti terlihat pada cara berikut.
Jawaban: D
Pembahasan selanjutnya mengenai materi jarak pada dimensi tiga adalah jarak titik ke garis.
Jarak Titik dan Garis
Jarak antara titik A ke garis <em>g< /em> adalah panjang garis tegak lurus titik A ke garis g. Sobat idschool perlu melakukan proyeksi titik A pada garis g terlebih dahulu. Tarik sebuah garis yang menghubungkan titik A pada garis g. Garis inilah yang menjadi jarak titik A ke garis g.
Untuk lebih jelasnya perhatikan gambar di bawah.

Proyeksi titik A pada garis g adalah A’
Berikutnya simak contoh soal jarak titik ke garis yang akan diberikan di bawah.
Contoh Soal dan Pembahasan Jarak Titik ke Garis
Diketahui kubus ABCD EFGH dengan panjang rusuk 6 cm. Jarak titik C ke garis FH adalah ….
A.
B.
C.
D.
E.
A.
B.
C.
D.
E.
Pembahasan:
Perhatikan gambar berikut!
Perhatikan gambar berikut!

Dengan mudah kita dapat mengetahui bahwa CH, CF, dan FH merupakan diagonal sisi. Sehingga dapat disimpulkan bahawa:
CH = CF = FH = diagonal sisi =  cm
cm
Selanjutnya, perhatikan segitiga CFH yang terdapat pada bangun ruang diatas, jika segitiga CFH digambar ulang akan terlihat seperti gambar berikut.
Selanjutnya, perhatikan segitiga CFH yang terdapat pada bangun ruang diatas, jika segitiga CFH digambar ulang akan terlihat seperti gambar berikut.

Jarak C ke FH = CC’ adalah
Jadi, jarak titik C ke garis FH pada kubus ABCD.EFGH dengan panjang rusuk 6 cm adalah  cm.
cm.
Pembahasan selanjutnya adalah jarak titik ke bidang.
Jarak Titik ke Bidang
Cara untuk menentukan jarak titik ke Bidang hampir sama dengan jarak titik ke garis. Langkah pertama yang harus dilakukan adalah melakukan proyeksi titik pada bidang terkait. Jarak titik ke bidang dinyatakan oleh jarak titik ke proyeksi titik pada bidang. Dengan kata lain dapat disimpulkan bahwa jarak antara titik A ke bidang  adalah panjang garis tegak lurus dari titik A ke bidang
adalah panjang garis tegak lurus dari titik A ke bidang  .
.
Perhatikan gambar di bawah dapat menggambarkan ilustrasi di atas untuk lebih jelasnya.

Jarak titik A pada bidang  sama dengan jarak AA’ dengan titik A’ merupakan titik proyeksi A pada bidang
sama dengan jarak AA’ dengan titik A’ merupakan titik proyeksi A pada bidang  .
.
Sekarang, latih pemahaman sobat idschool melalui contoh soal jarak titik ke bidang yang akan diberikan di bawah.
Contoh Soal dan Pembahasan Jarak Titik ke Bidang
Sebuah kubus ABCD.EFGH mempunyai panjang rusuk 6 cm, maka jarak titik D terhadap bidang ACH adalah …. (SOAL UN MATEMATIKA IPA 2016)
A.  cm
cm
B. cm
cm
C. cm
cm
D. cm
cm
E. cm
cm
B.
C.
D.
E.
Pembahasan:
Berdasarkan keterangan pada soal, dapat diperoleh gambar di bawah.

Jarak titik D terhadap bidang ACH sama dengan jarak DD’ di mana D’ merupakan titik proyeksi D pada bidang ACH yang terletak pada garis HH’.
BD = diagonal bidang =  cm
cm
Sehingga,
Selanjutnya,
Untuk langkah selanjutnya perhatikan segitiga HDH’ (siku-siku di D)!

Berdasarkan luas segitiga HDH’ akan diperoleh
Jadi, jarak D ke bidang ACH adalah  cm.
cm.
Jawaban: B
Perhitungan yang lumayan cukup panjang dan rumit, bukan?
Jangan khawatir, soal pada materi jarak pada dimensi tiga itu dapat dibilang unik. Misalnya, sobat tidak perlu menghitung diagonal sisi atau diagonal ruang pada suatu kubus. Karena, secara pasti, diagonal sisi suatu kubus adalah  dan diagonal ruang suatu kubus adalah
dan diagonal ruang suatu kubus adalah  .
.
Dengan banyak mengerjakan latihan berbagai jenis soal pada dimensi tiga, nantinya sobat idschool dapat memahami keunikan-keunikan materi jarak pada dimensi tiga. Jadi, kalau merasa kesulitan, jangan menyerah ya! Hehe.
Selanjutnya, kita akan masuk dalam pembahasan selanjutnya, yaitu jarak garis ke garis.
Jarak Garis ke Garis
Jarak antara dua garis atau jarak garis ke garis adalah panjang ruas garis yang menghubungkan antara garis pertama dan garis kedua, di mana ruas garis tersebut tegak lurus dengan garis pertama dan garis kedua. Cara yang harus dilakukan adalah mengambil sebuah titik yang merupakan bagian dari garis pertama. Kemudian, proyeksikan titik tersebut pada garis kedua. Sekarang dua titik tersebut terhubung oleh sebuah garis yang tegak lurus. Garis inilah yang menyatakan jarak garis ke garis.
Secara lebih detailnya, sobat idschool dapat melihat pada gambar di bawah.

Langsung saja, mari kita simak contoh soal dan pembahasan jarak garis ke garis.
Contoh Soal dan Pembahasan Jarak Antara Dua Garis (Jarak garis ke garis)
Perhatikan gambar berikut!

Diketahui panjang rusuk kubus di atas adalah 10 cm. Titik P dan titik Q berturut-turut merupakan titik tengah dari rusuk AB dan BC. Jarak garis PQ ke garis EG adalah ….
Pembahasan:
Perhatikan garis PQ dan garis EG!
Perhatikan garis PQ dan garis EG!

Jarak garis PQ terhadap garis EG sama dengan jarak titik M ke titik N.
Sebelum menentukan panjang MN, kita perlu mengitung panjang beberapa ruas garis terlebih dahulu.
PB = QB = 5 cm (P dan Q merupakan titik tengah masing-masing rusuk)
Mencari panjang PQ:
Berdasarkan teorema Phytagoras, maka dapat diperoleh panjang PQ dengan cara berikut.
Berdasarkan teorema Phytagoras, maka dapat diperoleh panjang PQ dengan cara berikut.
Mencari panjang QN:
Mencari panjang BN:
Berdasarkan teorema pythagoras (segitiga siku-siku di N)
Sehingga,
Berdasarkan teorema pythagoras (segitiga siku-siku di N)
Sehingga,
Mencari panjang FM:
FM merupakan setengah panjang diagonal sisi kubus (sisi EG), sehingga panjangnya adalah
FM merupakan setengah panjang diagonal sisi kubus (sisi EG), sehingga panjangnya adalah
Ingat!!!
Panjang diagonal sisi kubus adalah .
.
Panjang diagonal ruang kubus adalah .
.
Panjang diagonal sisi kubus adalah
Panjang diagonal ruang kubus adalah
Selanjutnya perhatikan gambar berikut!


Mencari panjang MF’:
Mencari Panjang MN:
Jadi panjang garis MN dengan garis EG adalah  cm.
cm.
Jawaban: E
Langkah yang cukup panjang. Pembahasan kita masih tersisa 2, yaitu jarak garis ke bidang dan jarak bidang ke bidang.
Jarak Garis ke Bidang
Jarak antara garis dan bidang merupakan jarak antara garis dengan garis proyeksinya pada bidang. Prinsip cara mencari jarak garis ke bidang hampir sama dengan mencari jarak garis ke garis. Bedanya, proyeksi pada jarak garis ke garis dilakukan antara garis ke garis, proyeksi garis ke bidang dilakukan antara garis ke bidang.
Untuk lebih jelasnya perhatikan gambar di bawah.

Sekarang, langsung saja simak contoh soal jarak garis ke bidang yang akan diberikan di bawah.
Contoh soal dan Pembahasan Jarak Garis ke Bidang
Diketahui panjang rusuk kubus di atas adalah 6 cm. Titik K, titik L, titik M, dan titik N berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan GH. Jarak garis KL ke bidang DMN adalah ….
A. 10 cm
B. 8 cm
C. 6 cm
D. 4 cm
E. 3 cm
Diketahui panjang rusuk kubus di atas adalah 6 cm. Titik K, titik L, titik M, dan titik N berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan GH. Jarak garis KL ke bidang DMN adalah ….
A. 10 cm
B. 8 cm
C. 6 cm
D. 4 cm
E. 3 cm
Pembahasan:
Perhatikan gambar berikut!

Keterangan:
Garis QR merupakan jarak antara bidang DMN dengan garis KL
DP tegak lurus dengan garis QR (karena QR adalah garis tinggi segitiga DQP)
KB = BL = =
=  cm
cm
Perhatikan gambar berikut!

Keterangan:
Garis QR merupakan jarak antara bidang DMN dengan garis KL
DP tegak lurus dengan garis QR (karena QR adalah garis tinggi segitiga DQP)
KB = BL =
Perhatikan segitiga KLB!


Mencari panjang KL:
Berdasarkan teorema pythagoras, maka dapat diperoleh panjang PQ dengan cara berikut.
Berdasarkan teorema pythagoras, maka dapat diperoleh panjang PQ dengan cara berikut.
Panjang QL =  KL =
KL =  =
=  cm (karena BQ adalah garis tinggi dan garis berat segitiga KLB).
cm (karena BQ adalah garis tinggi dan garis berat segitiga KLB).
Mencari panjang HP:
Berdasarkan teorema pythagoras maka dapat diperoleh persamaan di bawah.
Berdasarkan teorema pythagoras maka dapat diperoleh persamaan di bawah.
Panjang HP = BQ =  cm
cm
Mencari Panjang DQ:
Perhatikan gambar berikut!


Mencari panjang PF:
Sebelumnya, cari panjang HF terlebih dahulu, HF = diagonal sisi = .
.
Sebelumnya, cari panjang HF terlebih dahulu, HF = diagonal sisi =
Mencari panjang PQ:
Perhatikan kembali gambar berikut!


Mencari panjang DP:
Selanjutnya perhatikan gambar berikut!


Mencari panjang DO:
Mencari panjang QR:
Berdasarkan luas segitiga akan diperoleh hasil dari QR seperti terlihat pada cara berikut.
Berdasarkan luas segitiga akan diperoleh hasil dari QR seperti terlihat pada cara berikut.
Jadi jarak garis PQ ke bidang DRS adalah QR = 6 cm.
Jawaban: C
Jawaban: C
Done! proses yang sangat panjang.
Selanjutnya, kita akan masuk ke pembahasan terakhir yaitu jarak bidang ke bidang.
Jarak Bidang ke Bidang
Jarak antara dua bidang atau jarak bidang ke bidang adalah panjang ruas garis yang saling tegak lurus pada kedua bidang tersebut. Sama seperti pembahasan sebelumnya, sobat idschool perlu melakukan proyeksi titik yang merupakan bagian dari satu bidang ke titik lain yang merupakan bagian dari bidang ke dua.
Sehingga, jika kedua titik tersebut ditarik garis lurus akan saling tegak lurus dengan kedua bidang. Untuk lebih jelasnya, perhatikan gambar di bawah.

Berikut ini akan diberikan contoh soal bidang ke bidang.
Contoh Soal dan Pembahasan Jarak Bidang ke Bidang
Diketahui panjang sebuah rusuk kubus adalah 8 cm. Titik P, titik Q, titik R, dan titik S berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan HG. Jarak bidang FPQ ke bidang DRS adalah ….
A. 16 cm
B. 14 cm
C. 12 cm
D. 10 cm
E. 8 cm
Diketahui panjang sebuah rusuk kubus adalah 8 cm. Titik P, titik Q, titik R, dan titik S berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan HG. Jarak bidang FPQ ke bidang DRS adalah ….
A. 16 cm
B. 14 cm
C. 12 cm
D. 10 cm
E. 8 cm
Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh gambar dengan keterangan seperti terlihat pada gambar di bawah.

Jarak bidang FPQ ke bidang DRS sama dengan jarak titik ML. Sebelum menentukan nilai ML diperlukan beberapa langkah perhitungan terlebih dahulu seperti langkah-langkah berikut.
Menghitung panjang PQ:
PB = BQ = panjang rusuk kubus =
panjang rusuk kubus =  cm
cm
Sehingga, diperoleh persamaan PQ seperti di bawah.
PB = BQ =
Sehingga, diperoleh persamaan PQ seperti di bawah.
Segitiga PBQ adalah segitiga sama kaki, sehingga BM merupakan garis tingg dan garis berat garis PQ. Jadi PM = MQ = PQ =
PQ =  cm.
cm.
Mencari panjang BM (Perhatikan segitiga BMQ siku-siku di M):
Mencari panjang FM (Perhatikan segitiga FBM siku-siku di B):
Mencari panjang BD:
BD = diagonal sisi =
BD = diagonal sisi =
Mencari Panjang DM:
Perhatikan jajar genjang DMFK yang diambil dari gambar kubus sebelumnya.

Keterangan:
DM = FK = cm
cm
DK = FM = cm
cm
TK = BF = 8 cm
DM = FK =
DK = FM =
TK = BF = 8 cm
Mencari panjang ML:
